Summary

• The area ratio for pentagons is not constant.
• Regular pentagons have a ratio of 1/(4²).
• The conjectured maximum ratio for convex pentagons is 3/4.
• The general formula for the area of the midpoint polygon is (1/2)(Area of the Original Polygon) + (1/4)(Area of the Star Polygon), where the star polygon is constructed from the original by taking every other vertex in order.

Regular Pentagons and The Maximum Ratio

Now what about the areas of midpoint polygons for convex pentagons? For a regular pentagon (see figure 7), we note that the midpoint polygon is a similar figure to the original polygon. Thus, to find the area ratio, we need only take the square of the ratio of corresponding edges. In the figure, AC = 2FG and ED = AC, where is the golden section, about 0.618. The area ratio is therefore 1/(4²), or about 0.6545.

However for a pentagon close to a triangle, with two vertices close to one vertex on the bottom and two close to the other vertex on the bottom, the area of the midpoint figure is as close to 3/4 as we please (see demo 3 below). We have conjectured that this is the maximum ratio attainable for convex pentagons. Note that there is no upper bound to the area ratio for non-convex pentagons; see the original discussion for an example.

Before we look at pentagons in more detail, you may wish to look at similarly qualitative results for convex hexagons.

The General Formula For Pentagons

Surprisingly, although the area ratio for a pentagon is not constant, we can still find a relationship between the area of the original, the area of the midpoint polygon, and the area of another figure. This is first seen analytically, and later by a direct geometric argument.

Analytic Proof

For a quick overview of the notations and formulas used in this section, see the pages on oriented area and vector notation.

Recall that for a convex polygon with the origin in the interior, we can find the area by adding up the areas of the triangles with the origin as one vertex and a side of the polygon as the opposite side. If the coordinates of the ith vertex are (x_i,y_i), then the area of the ith triangle, with vertices (0,0), (x_i,y_i), (x_i+1,y_i+1) is

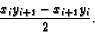
In vector notation, if (x_i,y_i) = X_i, then the area is

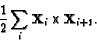
The vertices of the midpoint polygon on the other hand are Y_i = (1/2)(X_i+X_i+1) so the area of the midpoint polygon is

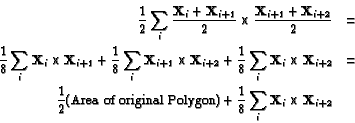
What is the meaning of the additional term? Formally, in the case of a pentagon, it represents 1/4 times the area of the polygon with vertices X₁, X₃, X₅, X₂, X₄. This is the so-called "star pentagon" formed by taking the five diagonals in sequence, a self-intersecting polygon. The sum of the five triangles will give the area of the star, but with the middle pentagon in the star counted twice.

This argument can be found in the original discussion here.

Geometric Interpretation

This is a geometric interpretation of the formula shown above: Area of Midpoint Polygon = (1/2)(Area of Original Polygon) + (1/4)(Area of Star Polygon). This was mentioned in the original discussion here (note that the comment was added several weeks after the other work on the page was submitted).

Below is a diagram of the star pentagon, shown in pink. The central pentagon, shaded darker than the rest of the star pentagon, is doubly covered (a phenomenon explained here). It is possible to interpret the analytic result above by tabulating the regions contained in the midpoint pentagon (partially shaded in gray).

Recall that the area of the midpoint pentagon is the sum of 1/2 the area of the original pentagon and 1/4 the area of the star pentagon. The midpoint pentagon contains 3/4 of the light pink triangular regions, 1/2 of the gray triangular regions, and all of the central pentagonal region. We can now sum up the regions directly to get these expected results:

We will find that this geometric construction works even for n-gons with n > 5, though the star polygon becomes a pair of disjointed polygons when n is even.